基于任务队列的线程运行模式
Chromium 除了远近闻名的多进程架构之外,它的多线程模型也相当引人注目的。Chromium 的多进程架构是为了解决网页的稳定性问题,而多线程模型则是为了解决网页的卡顿问题。为了达到这个目的,Chromium 的多线程模型是基于异步通信的。也就是说,一个线程请求另外一个线程执行一个任务的时候,不需要等待该任务完成就可以去做其它事情,从而避免了卡顿。
有同学看到这里可能会有疑问,如果一个线程请求另外一个线程执行一个任务的时候,就是要等该任务完成之后才能做其它事情,那么使用异步通信有什么用呢?的确如此,但是 Chromium 提供这种基于异步通信的多线程模型,就是希望作为开发者的你在实现一个模块的时候,尽最大努力地设计好各个子模块及其对应的数据结构,使得它们在协作时可以最大程度地进行异步通信。因此,Chromium 基于异步通信的多线程模型更多的是体现一种设计哲学。
一个典型的异步通信过程如图 1 所示: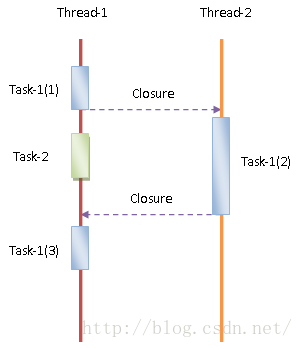
Task-1 被分解成三个子任务 Task-1(1)、Task-1(2) 和 Task-1(3)。其中,Task-1(1) 由 Thread-1 执行。Task-1(1) 执行完成后,Thread-1 通过我们在前面 Chromium 多线程通信的 Closure 机制分析一文分析的 Closure 请求 Thread-2 执行 Task-1(2)。Task-1(2) 执行完成后,Thread-2 又通过一个 Closure 请求 Thread-1 执行 Task-1(3)。至此,Task-1 就执行完成。我们可以将第一个 Closure 看作是一个 Request 操作,而第二个 Closure 是一个 Reply 操作,这是一个典型的异步通信过程。当然,如果不需要知道异步通信结果,那么第二个 Closure 和 Task-1(3) 就是不需要的。
假设 Thread-1 需要知道异步通信的结果,那么在图 1 中我们可以看到一个非常关键的点:Thread-1 并不是什么也不干就只是等着 Thread-2 执行完成 Task-1(2),它趁着这个等待的空隙,干了另外一件事情——Task-2。如果我们将 Thread-1 看作是一个 UI 线程,那么就意味着这种异步通信模式是可以提高它的响应性的。
为了能够完成上述的异步通信过程,一个线程的生命周期如图 2 所示: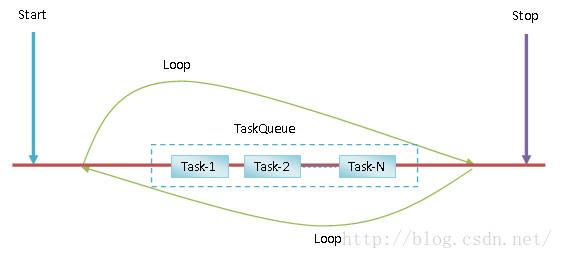
线程经过短暂的启动之后(Start),就围绕着一个任务队列(TaskQueue)不断地进行循环,直到被通知停止为止(Stop)。在围绕任务队列循环期间,它会不断地检查任务队列是否为空。如果不为空,那么就会将里面的任务(Task)取出来,并且进行处理。这样,一个线程如果要请求另外一个线程执行某一个操作,那么只需要将该操作封装成一个任务,并且发送到目标线程的任务队列去即可。
为了更好地理解这种基于任务队列的线程运行模式,我们脑补一下另外一种常用的基于锁的线程运行模式。一个线程要执行某一个操作的时候,就直接调用一个代表该操作的一个函数。如果该函数需要访问全局数据或者共享数据,那么就需要进行加锁,避免其它线程也正在访问这些全局数据或者共享数据。这样做的一个好处是我们只需要关心问题的建模,而不需要关心问题是由谁来执行的,只要保证逻辑正确并且数据完整即可。当然坏处也是显然的,首先是为了保持数据完整性,也就是避免访问数据时出现竞争条件,代码里面充斥着各种锁。其次,如果多个线程同时获取同一个锁,那么就会产生竞争。这种锁竞争会带来额外的开销,从而降低线程的响应性。
基于任务队列的线程运行模式,要求在对问题进行建模时,要提前知道谁是执行者。也就是说,在对问题进行建模时,需要指派好每一个子问题的执行者。这样我们为子问题设计数据结构时,就规定这些数据结构仅仅会被子问题的执行者访问。这样执行者在解决指派给它的问题时,就不需要进行加锁操作,因为在解决问题过程中需要访问的数据不会同时被其它执行者访问。这就是通过任务队列来实现异步通信的多线程模型的设计哲学。
当然,这并不是说,基于任务队列的线程运行模式可以完全避免使用锁,因为任务队列本身就是一个线程间的共享资源。想象一下,一个线程要往里面添加任务,另一个线程要从里面将任务提取出来处理。因此,所有涉及到任务队列访问的地方都是需要加锁的。但是如果我们再仔细想想,那么就会发现,任务队列只是一个基础设施,它与具体的问题是无关的。因此,只要我们遵循上述设计哲学,就可以将代码里面需要加锁的地方仅限于访问任务队列的地方,从而就可以减少锁竞争带来的额外的开销。
这样说来,似乎基于任务队列的线程运行模式很好,但是实际上它对问题建模提出了更高的要求,也就是进行子问题划分时,要求划分出来的子问题是正交的,这样我们才有可能为这些子问题设计出不会同时被访问的数据结构。看到“正交”两个字,是不是想起高数里面的向量空间的正交基了?或者傅里叶变换用到的一组三角函数了?其实道理就是一样一样的。